Flat or Lumpy – How Would You Like Your Insulation?

My dissertation in grad school was called “Flat or Lumpy.” (Of course, it had the requisite incomprehensibility in the subtitle, with words like ‘heteroepitaxy.’) Those two words in the title, which cut to the heart of what my surface physics research was all about, also describe a property of insulation that’s important in building science.
Let me put the question to you this way. If your attic is going to have 50 bags of insulation blown into it, does it make much of a difference if it goes in flat or lumpy?
Let’s look at an example. If the insulation goes in perfectly flat, let’s say we have a nice uniform R-value of 30 throughout the attic. (We’re going to ignore the complicating factor of the framing and assume it’s a continuous layer of blown insulation.)
There are all kinds of ways it can go in lumpy, but let’s assume that 50% of the attic has lumps of R-50 insulation, and the other 50% is valleys with only R-10. We want to find the average R-value of this lumpy configuration. It’s the same amount of insulation, and the average of R-50 and R-10 is R-30. But, how does it really perform?
Let’s do the math!
[Warning: This section contains mathematics. If you feel nausea or dizziness, skip to the conclusion below. If you feel excited by this discussion, see your local physics department. If your arousal lasts longer than 4 hours, you should work through the problems in Classical Electrodynamics by J.D. Jackson.]Now, we can’t just average the R-values. If we did that here, we’d get R-30, and we’d be wrong. Heat will take the path of least resistance, and the less resistance you give it, the more heat will flow. If you’ve studied physics, engineering, or building science, you’ve probably seen the equation for heat flow by conduction:
If we calculated the amount of heat flowing through the lumps and valleys in this attic, we’d see that the R-10 half (red bar below) would allow way more heat to flow than the R-50 half (yellow bar below). In fact, the R-10 valleys, having one-third the R-value, would allow 3 times more heat to flow than if it had R-30. The R-50 lumps would allow only 3/5 the heat flow as R-30.
Also, the total amount of heat flow is greater for the lumpy insulation than for the flat insulation. As you can see below, the red and yellow parts together add up to a lot more heat flow than the orange (actually 1.8 times as much).
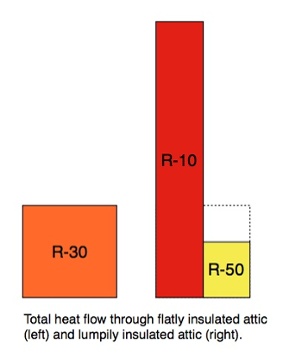
Because the lumpy insulation allows more heat flow, it’s got to have a worse average R-value. Clearly, the average R-value is going to be more influenced by the underinsulated part than by the overinsulated part.
To find the average R-value the correct way, we first have to convert R-values to U-values. R stands for resistance, as in resistance to heat flow, so the higher the number the better when we’re talking about building materials. U-value, the heat transfer coefficient, is the reciprocal of the R-value, so the lower the number, the better. (For a better understanding, see this Wikipedia article about R-value and U-value.)
The equation for average U-value is:
Taking the attic as 1000 square feet total and putting in 1/R for U, we get:
Taking the reciprocal of 0.06, we get the average R-value of about 17, which is much lower than the R-30 we’d get by incorrectly averaging the R-values.
Conclusion
As I said above, heat takes the path of least resistance, so the amount of extra heat going through the R-10 half far exceeds the extra heat flow that’s stopped on the R-50 side. Instead of getting an R-30 average, the lumpy attic has an R-17 average.
In practical terms, this means that if you see an attic with lumpy insulation, get in there with a rake and smooth it out. In the example I just worked out, you’d nearly double the R-value without adding any extra insulation!
Another common example of the flat-or-lumpy conundrum is an attic that’s perfectly insulated except for one small area, say the pull-down attic stairs. We can go through the same steps as above and show that an attic that has a uniform R-30 over 99% of the area and 1% at R-1 (the pull-down stairs) will have an average R-value of 23.
That’s right, those pull-down stairs can decrease your overall R-value by 25%. One small uninsulated area reduces the R-value dramatically.
In my graduate research, getting smooth, flat layers was our goal. In the building science of insulation, flat also wins out over lumpy.
This Post Has 8 Comments
Comments are closed.

I know a couple who had an
I know a couple who had an opossum in their crawl space and walls. The insulation under their floor sure did get moved around: it was lumpy.
Your math sounds like a good reason to get foam insulation, which is not likely to get moved around by our animal friends.
Excellent commentary, Allison
Excellent commentary, Allison … had assumed your conclusion but nice to have the equations to back it up … attic stair insulation/encapsulation should be an easy sell.
Great stuff Allison.
Great stuff Allison.
Elaine, yes, spray foam might
Elaine, yes, spray foam might help, but keeping animals out of the crawl space would be the first step. Depending on their house, they might also want to consider crawl space encapsulation.
Thanks, Paul & Jamie. It’s just basic physics, but it surprises a lot of people to find out stuff like this.
Our animal friends may not
Our animal friends may not move the foam insulation around, but if an animal of a spray foam contractor sprays your foam you could have the same issue. I know of an attic (not mine of course) that has up to 9″ of foam in some areas and as little as 0.5″ in others. This could have the same effect…..could it not?
Chris, as a matter of fact, I
Chris, as a matter of fact, I wrote this article because of the very issue you raise. I wanted to write an article about problems with spray foam, one of them being uneven distribution of the foam, but then I realized I needed an article before that explaining why uneven distribution was so bad. So, I wrote this article on 6/28 and the spray foam article on 6/29. In fact, the video in that spray foam article has exactly the kind of installation you described. It’s almost like you know where I filmed that video.
So I suppose the same
So I suppose the same principle would apply to some insulated concrete forms, where a proportion of the insulation is full width (e.g. 8 inches) and a proportion is only an inch or two either side of a concrete column? And to whole wall R-value calculations for wood framed walls? But even more complicated when you introduce non-linear thermal bridging e.g. steel studs.
Andy P:
Andy P: You got it.