The Magic of Cold, Part 2 – Intermediate Air Conditioning Principles

Yesterday, I wrote about the refrigeration cycle for beginners. (Another good article that covers basics of the refrigeration cycle as well as answers to some commonly asked questions is Martin Holladay’s Air Conditioner Basics.) Today we go a little deeper. This will be the intermediate version of how your air conditioner works, and I’ll name the parts of the refrigeration cycle and talk a little bit more about the changes in the refrigerant as it goes through the cycle.
Still, there’s a lot I’m not going to cover in this article. I’m not going into the technical details of checking refrigerant levels, the properties of the different refrigerants used, how efficiency (SEER rating) is calculated, or any number of other important aspects of air conditioning systems.
The Refrigeration Cycle
The way your air conditioner pumps heat from inside to outside is through the refrigeration cycle, a thermodynamic cycle involving a special fluid – the refrigerant – that undergoes phase changes (between liquid and vapor), pressure changes, and temperature changes. The diagram below shows how the refrigerant flows through the air conditioning system and what’s happening along the way.
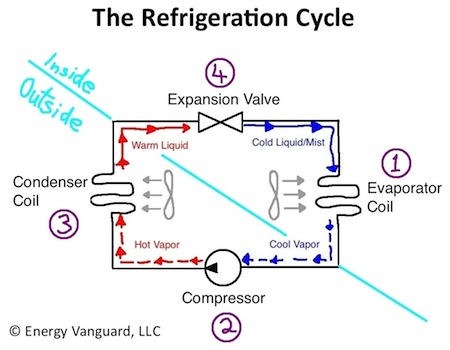
First, notice that the diagonal line shows which parts are inside the house and which parts are outside. If you have a split system, with the condensing unit sitting outside making noise and the air handler inside (which could mean in the crawl space or attic), the components are in different boxes. In a window AC or package unit, they’re all in the same box.
Now, let’s go through the four stages of the refrigeration cycle, one by one.
1. Evaporator Coil
This is where the refrigerant picks up heat from inside the house. The evaporator coil is a copper tube, which carries the refrigerant, embedded in a framework of aluminum fins (photo below). Using this configuration, the refrigerant is connected to a lot of surface area that makes contact with the air blowing over it, which aids heat transfer from the air to the refrigerant. The most common geometry is the A-coil (below), but you also see flat coils and N-coils in some units.

The refrigerant comes into the evaporator coil as a liquid at a low temperature and low pressure. The air handler’s fan (aka the blower) blows air from the house across the coil. The evaporator coil is cold (about 40° F), and the air from the house is warm (about 75° F, depending on where you set your thermostat). Heat flows from warmer to cooler, so the air temperature drops, and the refrigerant picks up the heat lost by the air. This is the second law of thermodynamics in action.
In addition to getting warmer, the refrigerant also changes phase here. It’s called the evaporator coil, after all, so the cold liquid refrigerant coming in evaporates and becomes a vapor. Phase changes are a great way to transfer heat because it takes a lot more heat to cause a phase change (especially between liquid an vapor) than it does to change the temperature of a material. Thus, when the refrigerant starts boiling, it really sucks up the Btu’s (British Thermal Units).
One aspect of the flow may be confusing when you look at your air conditioner and try to figure out how the refrigerant flows from inside to outside. If you have a split system, the inside and outside pieces are connected by the refrigerant lines. These are two copper tubes, one larger and insulated tube (the suction line) running parallel to another smaller and uninsulated tube (the liquid line). When the vaporized refrigerant leaves the evaporator coil, it’s still fairly cold. Hence, the refrigerant going to the compressor outside is in the larger, insulated copper tube, not the smaller, warmer tube. As paradoxical as it seems, the colder tube is the one carrying the most heat. You can see this in the photo at right because the suction line even has frost on it, which is not normal and indicates a problem.
another smaller and uninsulated tube (the liquid line). When the vaporized refrigerant leaves the evaporator coil, it’s still fairly cold. Hence, the refrigerant going to the compressor outside is in the larger, insulated copper tube, not the smaller, warmer tube. As paradoxical as it seems, the colder tube is the one carrying the most heat. You can see this in the photo at right because the suction line even has frost on it, which is not normal and indicates a problem.
2. Compressor
When the refrigerant reaches the outdoor part of your air conditioner (photo at top), the compressor does exactly what its name suggests – it squishes the refrigerant down to a smaller volume, thus increasing the pressure and the temperature. Why? Because heat flows from warmer to cooler. You can’t get rid of heat from a cold refrigerant to 95° F air. The refrigerant has to be warmer than the outside air. That’s one reason why we need the compressor. The other is that the compressor is the pump that moves the refrigerant through the system.
3. Condenser coil
When the high pressure, high temperature, vaporized refrigerant leaves the compressor, it enters the condenser coil. Again, it’s a copper tube embedded in aluminum fins that allows for efficient heat transfer. A fan inside the condensing unit pulls outdoor air through the sides of the coil and blows it out the top of the unit. Because of the work the compressor did, the refrigerant is hotter than the outdoor air. The second law of thermodynamics kicks in here, and heat flows from the warmer refrigerant to the cooler outdoor air blowing over the condenser coil.
In the evaporator coil, refrigerant changes from liquid to vapor at a relatively low temperature. Now we’re dealing with higher temperatures, and the phase change reverses. If you’re confused by the phase change happening at different temperatures, think about what happens when you go to high altitudes. The air pressure is lower, and water boils at less than 212° F. Pressure changes affect the boiling/condensation point temperature, which is why boiling happens at a low temperature in the evaporator coil and condensation happens at a high temperature in the condenser coil.
After returning to the liquid state, the refrigerant travels through the liquid line (the hot, uninsulated copper tube) back to the indoor part of the air conditioner.
4. Expansion Valve – Where the Magic Happens!
Once the refrigerant gets back to the indoor unit, it passes through the expansion valve, and the magic of the refrigeration cycle happens here. The high pressure, relatively warm liquid runs into a constriction that doesn’t allow the refrigerant to pass through easily. As a result, when the liquid does get through to the other side, it finds itself in a much lower pressure. When the pressure drops like this, so does the temperature – a lot! This is what makes air conditioning possible. Without being able to get the refrigerant down to temperatures below the air in your home, an air conditioner wouldn’t be able to work. Why? Because heat flows from warmer to cooler, the old second law of thermodynamics again.
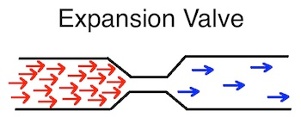
After passing through the expansion valve, the refrigerant goes directly into the evaporator coil, and the cycle begins anew.
To read a simplified version of this article, see:
The Magic of Cold, Part 1 – How Your Air Conditioner Works
Allison Bailes of Atlanta, Georgia, is a speaker, writer, building science consultant, and the founder of Energy Vanguard. He has a PhD in physics and writes the Energy Vanguard Blog. He is also writing a book on building science. You can follow him on Twitter at @EnergyVanguard.
Related Articles
How the Heck Does a Heat Pump Get Heat from Cold?!
Can You Oversize a Mini-Split Heat Pump?
3 Reasons Your 3 Ton Air Conditioner Isn’t Really 3 Tons
NOTE: Comments are closed.
This Post Has 7 Comments
Comments are closed.

Clear as part 1 <
Clear as part 1
I evoke the second law of thermodynamics in all of my discussions with my customers. It really helps them understand how their home works.
Keep it up
Allison, another clear and
Allison, another clear and enlightening article… thanks.
Carl: The
Carl: The second law of thermodynamics is one of the most important principles of all. You have to be a little careful about how much you say, though. Too much thermodynamics has been known to lead to suicide.
Tom: Glad you liked the article!
To whom it may concern;&
To whom it may concern;
Due to alot of thermodynamics I have decided I can’t live any longer with out it. I’ve tried my best and no matter what I have done,… It always gets to me and burns me up!
Good explanation of the magic of cool/AC! Now if I could only get someone to explain to me on how to still be cool at my age as you can see by this post, Lol.
Thanks AB3!
u have explaind you’re self
u have explaind you’re self better than my ex instructor . u just made my life easier.thank u
Everything that is lost in
Everything that is lost in the 2nd law can be found hiding in the entropy.
Hi Allison,
Hi Allison,
Very good article, with just the right amount of detail to explain the underlying concepts and illustrate how an air conditioning system works.
This article is over 3 years old so I don’t know if you are still accepting comments, but I have a question related to the photo in your article where ice has formed on the suction line. You mentioned that this is a sign of a problem, and in fact this happened to my ac system once when I ran low on refrigerant. I’m having trouble understanding why that happens. Intuitively, I would think that the less refrigerant in the line, the HIGHER the temperature would be and the less likely it would be to form ice. Unless it has to do with pressure: the less refrigerant in the lines the less pressure there is and it can’t get hot enough to keep ice from forming (higher pressure = higher heat, right?). Any explanation you can offer would be appreciated.
Thanks,
Mike